【湖畔光影】数学校本研修之课例研讨（120）——由应用入手，架构教学设计

【课前慎思】

两种相关联的量，对应的比的比值一定，就说这两种量成正比例关系，这两种量是成正比例的量。根据正比例的意义，常常要判断两种量是不是成正比例关系。因此，我在设计本节课的时候，就尝试由应用入手，完成教学设计。

应用之一：算比值来判断

根据正比例的意义，当看到一组数据，怎么判断两种量是不是成正比例关系呢？

可以计算对应比的比值。如果比值均相等，则两种量成正比例；如果对应比的比值不相等，则两种量不成正比例。

应用之二：析关系来判断

有的时候，没有数据，仅有一句话概括一组关系，则需要能够根据数量之间的关系来判断。比如，速度一定，路程和时间成不成正比例。因为路程：时间=速度，已知速度一定，所以当速度一定，路程和时间成正比例。

应用之三：看图像来判断

除了算比值、析关系，还可以怎么来判断呢？

我们尝试在图上画出成比例关系的两种量所形成的图形，发现是一条直线。于是，又增加了一种判断两种量是不是成正比例关系的方法，那就是看是不是成直线。

以上即为围绕应用循序渐进展开的教学设计，那么，究竟依此设计组织教学的课堂究竟是什么样的呢？以下就请随我走进《正比例的意义》的课堂。

【课堂实录】

一、由数据入手，探究和揭示正比例关系

1.阅读表格，整理信息

（1）课件出示下列表格。

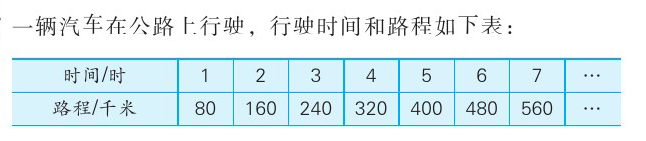
（2）引导学生阅读表格，说一说：从表格中可以知道哪些信息？

生：一辆汽车1小时行驶80千米，2小时行驶160千米，3小时行驶240千米，4小时行驶320千米，5小时行驶400千米，6小时行驶480千米，7小时行驶560千米。

2.根据数据，探究关系。

（1）说一说：什么是“两种相关联的量”？

师：有了表格中的这些数据，数学上就说路程和时间是两种相关联的量，你能结合这些数据说一说为什么吗？

板贴：时间变化，路程随着变化。路程和时间是两种相关联的量。

（2）找一找：还有哪两种量也是“相关联的量”？

（3）比一比：都是“两种相关联的量”，有什么不同？

板贴：有些变化方向相同，例如路程是时间；

有些变化方向不同，例如每组人数和组数。

（4）算一算：路程和相对应的时间组成的比的比值。

师：再回到这张表格。我们通过观察，发现路程和时间是两种相关联的量。那么，除此之外，还能有什么发现呢？

生：路程和相对应的时间组成的比的比值相等，都是80。

板书：

80:1=80

160:2=80

240:3=80

……

560:7=80

板贴：路程和时间的比的比值相等。

师：路程和时间是两种相关联的量，并且，路程和相对应的时间组成的比的比值都相等，数学上就说路程和时间成正比例关系，路程和时间是两种成正比例关系的量。

板贴：路程和时间成正比例关系。路程和时间是成正比例关系的量。

3.回顾过程，提炼方法。

师：回顾以上过程，我们是怎样得出路程和时间成正比例关系的呢？

生：我们先通过观察数据，发现路程和时间是两种相关联的量，再通过计算，发现路程和对应的时间组成的比的比值相等，最后推理得出路程和时间成正比例关系，路程和时间是两种相关联的量。

师：也就是结论的得出，经历了先观察再判断的过程。那么，两种相关联的量是不是一定对应比的比值相等呢？

生：不是。

师：你能举例说明吗？

生：……

师：两种相关联的量，不一定就对应比的比值相等。那么，如果两种量对应比的比值相等，是不是说明这两种量就是相关联的量呢？

生：是的。

生：因为一种量变化，另一种量也随着变化，才有可能对应比的比值相等。

师：因此，刚才推理路程和时间成正比例的过程可以简化。简化成做什么呢？

生：算路程和时间对应比的比值，看是不是相等。

4.练习判断，巩固方法。

课件出示下图：

购买一种铅笔的数量和总价如下表：

铅笔的总价和数量成正比例吗？为什么？

师：你想怎么判断？

生：算出总价和数量对应比的比值，看是不是相等。

师：可行吗？试试看。

……

师：有结论了吗？谁来说一说？

生：0.4:1=0.4,0.8:2=0.4,1.2:3=0.4……

总价和数量对应比的比值相等，所以总价和数量成正比例。

二、梳理比值含义，掌握关系本质

1.分析对应比的比值，掌握成正比例关系的本质。

课件同时出示下列两张表格：

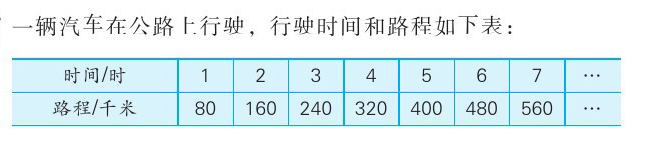
师：我们通过计算，推理得出路程和时间成正比例，总价和数量成正比例。那么，如果没有这些表格和数据，我们还能不能判断路程和时间、总价和数量之间的关系呢？

生：……

师：我们来继续研究。路程和时间对应的比的比值相等，就可以判断路程和时间成正比例，那么，路程和时间对应比的比值叫什么？

生：速度。

师：是的，路程和时间对应比的比值是速度。因此，路程和时间对应比的比值相等，也就是路程除以时间等于速度，速度一定。当速度一定时，就说路程和时间成正比例关系。

师：再来看看总价和数量。可以怎么判断？

生：单价一定，总价和数量成正比例。

师：为什么？你是怎么想的？

生：因为总价与数量的比的比值是单价，单价一定，也就是总价和数量的比的比值相等，所以总价和数量成正比例。

2.由上述判断过程提升方法，统一表示。

师：x和y表示两种相关联的量，什么情况下，x和y成正比例？

生：x和y比值一定。

师：我们用字母k表示x和y的比值，用一个什么样的式子就能表示x和y成正比例了呢？

板书：Y:x=k（一定），x和y成正比例关系。

三、列举更多例子，强化对正比例关系的认识

1.找一找：生活中还有哪两种量也成正比例关系？

师：这里的x和y可以表示路程和时间，k表示速度，x和y也可以表示总价和数量，k表示单价，那么，x和y还可以表示哪两种量呢？

先自己想一想，再和身边的同学说一说，最后指名口答，集体交流。

2.判一判：下列两种量是不是成正比例？

（1）正方形的周长和边长。

（2）人的身高和年龄。

（3）圆的周长和直径。

1. 借助图形，进一步丰富判断方法

1.回顾过程，提出问题。

师：我们一起回顾上述判断过程，怎样判断两种量是不是成正比例关系呢？

如果有数据，可以怎样做？

生：算比值。

师：如果没有数据呢？

生：找关系。

师：那除了算比值和找关系，还有没有其他判断方法呢？

2.数形结合，丰富方法。

师：著名数学家华罗庚先生说过一句话，大家一起读一读！

生：数缺形时少直观， 形少数时难入微。数形结合百般好，隔离分家万事休。

师：我们学到数，要想到形。那么，图形对于我们判断两种量是不是成正比例关系，有没有帮助呢？

课件出示坐标图。

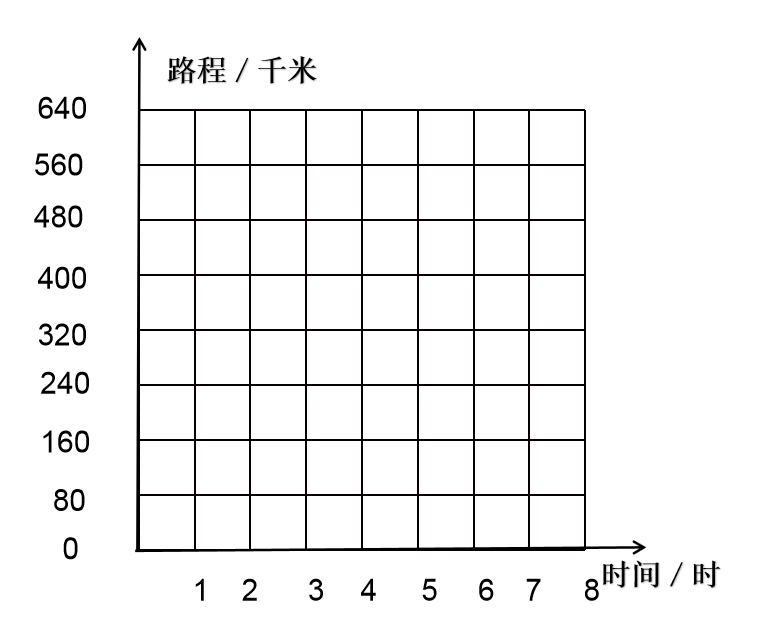
师：这是一张坐标图，横轴表示时间，纵轴表示路程。1小时行驶80千米，可以用一个点表示，这个点在哪里？谁去指一指？

师：2小时行驶160千米，也可以在图上找到一个点，是哪个点？谁去指一指？

师：像这样，剩下的3小时行驶240千米……直到7小时行驶560千米，都可以分别用一个点来表示。我们把这些点全部连接起来，看到了什么？

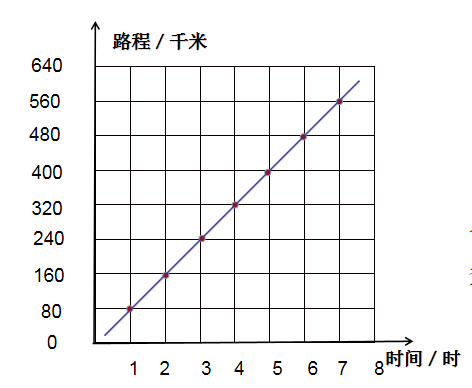
生：一条直线。

师：是的，成正比例关系，图像是一条直线。

3.及时应用，巩固认识。

课件出示下题：

小军和家人周末骑车去森林动物园游玩。下面的图像表示他们骑车行的路程和时间的关系。

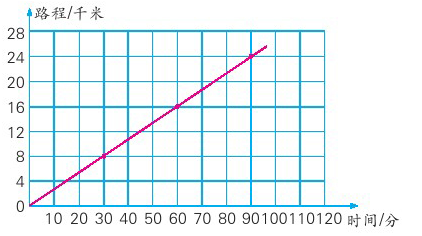
他们骑车行的路程和时间成正比例吗？为什么？

4.再次回顾，总结完善。

师：我们再来回看判断两种量是不是成正比例。如果有数据，可以算比值；如果没有数据，可以找关系。还可以怎么判断呢？

生：看图像。

五、全课总结

师：本节课，我们学习了哪些内容？可以看着板书，回想课件，来说一说。

六、当堂测评

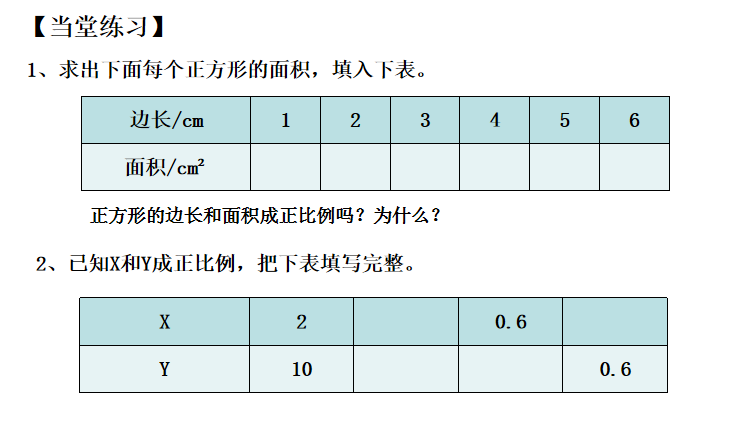
【课后回顾】

课后，结合课堂教学实际情况对教学设计再进行回顾，发现有以下方面需要进一步改进：

一、为谁优化？

在本节课中，针对逐步呈现的条件-两种相关联的量以及对应比的比值一定，我力图引导学生厘清这两个条件之间的包含关系，即如果“两种量对应比的比值一定”，则“两种量一定是两种相关联的量”，从而可以将两个条件都强调一遍简化和优化为只强调第二个条件—两种相关联的量的对应比的比值一定。理想很丰满，现实很骨感，从课堂上学生在这个环节的“顽固”表现来看，学生并未认同和接受如此优化。

原因何在？怎么改进？

仔细回看课堂视频，发现可能与自己在这个部分所用的教学方式比较单一有关。如何改进？我想可以通过加强对比来帮助学生理解和认同，另外，通过反复判断，也会加深学生对此两种条件之间关系的认识，然后渐渐达成通过优化以凸显本质的学习目标。

二、肢体语言

视频录制成功，在播放给组内同伴观看之前，我已经自行观看过4遍，并根据课堂视频进一步修改了教学设计。

在反复观看的过程中，发现本节课自己的肢体语言，特别是手上动作过于丰富，需要精减。这也是需要自我改进和完善的方面。

昨天，阅读贲友林老师发表在《教育视界》上的随笔，讲到独立备课的重要性。这节课也是我独立备课，试上修改所成。一定还存在很多不尽如人意的地方，但是，从独立思考开始，基于学生学情设计课堂教学，则是更加重要的、旨在提升师能的要求。

教无定法，贵在得法。让我们共同努力，让自己因愈得法而愈自由，最终能够从教学中享受到越来越多的职业幸福。

撰稿：华琴